Look at java and CPU caches
Memory hierarchy
Рассмотрим иерархию кешей и время доступа к данным. Время зависит от hardware и приведено для наглядности во сколько раз каждая память быстрее или медленнее другой.
Processor registers
Регистры процессора имеют самый быстрый доступ (обычно 1 цикл процессора) и могут иметь размер до нескольких байт.
L1 cache
Кэш L1 (кэш инструкций и кэш данных) обычно имеет размер 128 килобайт. Время доступа составляет около 0,5 наносекунды для кэша данных и 5 наносекунд для кэша инструкций при ошибочном предсказании ветвления.
L2 cache
Кэши L2 - кэш инструкций и кэш данных (общий) - размеры здесь различны, но могут составлять от 256 килобайт до 8 мегабайт. Обращение к кэшу L2 занимает около 5-7 наносекунд.
L3 Cache
L3 - это разделяемый кэш. Размер кэша L3 может варьироваться от 32 до 64 мегабайт. Кэш L3 является самым большим, но и самым медленным - время доступа к нему составляет около 12 наносекунд. Кэш L3 может находиться в самом процессоре, однако для каждого ядра соответствуют кэши L1 и L2, в то время как кэш L3 является общим для всех ядер CPU.
Main memory
Основная память (первичная память) - ее объем варьируется от 16 до 256 гигабайт. Время доступа составляет около 60 наносекунд.
Disk storage
Дисковая память (вторичная память) - ее объем достигает терабайта. Для твердотельных накопителей скорость доступа составляет около 100 микросекунд, а для нетвердотельных - около 300 микросекунд.
CPU cache access
Что бы понять влияние кеша на исполнение проведем эксперимент. Сперва определим массив с 64 1024 1024 целочисленными элементами. Далее определим два цикла, первый из которых выполняет итерацию и умножение каждого элемента в массиве. Второй цикл выполняет итерацию и умножение каждого 16-го элемента. Какая реализация быстрее и во сколько раз? Второй цикл в 1/16 часть времени быстрее, не так ли?
@State(Scope.Thread)
@BenchmarkMode(Mode.AverageTime)
@Warmup(iterations = 2, time = 1, timeUnit = TimeUnit.SECONDS)
@Measurement(iterations = 2, time = 1, timeUnit = TimeUnit.SECONDS)
@Fork(2)
@OutputTimeUnit(TimeUnit.MILLISECONDS)
public class CpuCache {
private static final int ARRAY_SIZE = 64 * 1024 * 1024;
public int[] array;
@Setup(Level.Iteration)
public void setUp() {
array = new int[ARRAY_SIZE];
Arrays.fill(array, 1);
}
@Benchmark
public void baseline() {
}
@Benchmark
public void accessfieldby_1(Blackhole bh) {
for (int i = 0, n = array.length; i < n; i++) {
array[i] *= 3;
}
}
@Benchmark
public void accessfieldby_16(Blackhole bh) {
for (int i = 0, n = array.length; i < n; i+=16) {
array[i] *= 3;
}
}
}
Consider result of benchmarks.
Benchmark Mode Cnt Score Error Units
CpuCache.accessfieldby_1 avgt 4 18.675 ± 2.091 ms/op
CpuCache.accessfieldby_16 avgt 4 18.702 ± 0.447 ms/op
CpuCache.baseline avgt 4 ≈ 10⁻⁶ ms/op
Почему умножение каждого 16-го элемента занимает столько же времени, сколько и умножение каждого элемента? Второй цикл выполняет лишь часть работы, так как же возможно, что первый цикл работает с той же скоростью? Ответ кроется в том, как процессор использует кэш-память и поэтому мы берем каждый 16-й элемент. На моем PC кэш-память L1 содержит кэш данных и кэш инструкций по 32 кБ на ядро, размер строки кэша - 64 байта.
kyryl-rybkin@pc:~$ lscpu | grep "cache"
L1d cache: 192 KiB (6 instances)
L1i cache: 192 KiB (6 instances)
kyryl-rybkin@pc:~$ getconf -a | grep CACHE
LEVEL1_ICACHE_SIZE 32768
LEVEL1_ICACHE_ASSOC
LEVEL1_ICACHE_LINESIZE 64
LEVEL1_DCACHE_SIZE 32768
LEVEL1_DCACHE_ASSOC 8
LEVEL1_DCACHE_LINESIZE 64
Как видно cache line на моем PC занимает 64 байта. В последовательном мы преобразуем каждый элемент в массиве, при итерации по кадому 16 элементу мы преобразуем один элемент с cache line. т.к. кеш L1 достаточно быстр, то можно получить примерно такое же количество операций в секунду.
Размер данных для L1, L2, и L3 кешей
Рассмотрим, влияет ли размер структуры данных на производительность программного обеспечения во время выполнения. Можно провести небольшой эксперимент. Во-первых, определим размер массива в качестве параметров для эталона. Во-вторых, определим цикл, который будет оценивать массив и выполнять тривиальные операции, например, умножение на 3 в каждой строке кэша.
@State(Scope.Thread)
@BenchmarkMode(Mode.AverageTime)
@Warmup(iterations = 5, time = 1, timeUnit = TimeUnit.SECONDS)
@Measurement(iterations = 5, time = 1, timeUnit = TimeUnit.SECONDS)
@OutputTimeUnit(TimeUnit.NANOSECONDS)
public class ArraySize {
private static final int ARRAY_CONTENT = 777;
@Param({"1024", "2048", "4096", "8192", "16384", "32768", "65536", "131072", "262144", "524288", "1048576", "2097152", "4194304", "8388608", "16777216", "33554432", "67108864", "134217728", "268435456", "536870912"})
public int size;
public int[] array;
public int counter;
public int mask;
@Setup(Level.Iteration)
public void setUp() {
final int elements = size / 4;
final int indexes = elements / 16;
mask = indexes - 1;
array = new int[elements];
Arrays.fill(array, ARRAY_CONTENT);
}
@Benchmark
public void benchLoop() {
array[16 * counter] *= 3;
counter = (counter + 1) & mask;
}
}
Benchmark (size) Mode Cnt Score Error Units
ArraySize.benchLoop 1024 avgt 25 1.296 ± 0.001 ns/op
ArraySize.benchLoop 4096 avgt 25 1.303 ± 0.009 ns/op
ArraySize.benchLoop 8192 avgt 25 1.297 ± 0.021 ns/op
ArraySize.benchLoop 32768 avgt 25 1.357 ± 0.058 ns/op
ArraySize.benchLoop 49152 avgt 25 1.345 ± 0.036 ns/op
ArraySize.benchLoop 65536 avgt 25 1.417 ± 0.039 ns/op
ArraySize.benchLoop 98304 avgt 25 1.320 ± 0.026 ns/op
ArraySize.benchLoop 131072 avgt 25 1.415 ± 0.019 ns/op
ArraySize.benchLoop 196608 avgt 25 1.415 ± 0.037 ns/op
ArraySize.benchLoop 229376 avgt 25 1.398 ± 0.027 ns/op
ArraySize.benchLoop 262144 avgt 25 1.542 ± 0.029 ns/op
ArraySize.benchLoop 393216 avgt 25 1.411 ± 0.037 ns/op
ArraySize.benchLoop 524288 avgt 25 1.610 ± 0.034 ns/op
ArraySize.benchLoop 1048576 avgt 25 1.636 ± 0.025 ns/op
ArraySize.benchLoop 1572864 avgt 25 1.668 ± 0.063 ns/op
ArraySize.benchLoop 2097152 avgt 25 1.920 ± 0.038 ns/op
ArraySize.benchLoop 6291456 avgt 25 1.917 ± 0.036 ns/op
ArraySize.benchLoop 8388608 avgt 25 3.327 ± 0.109 ns/op
ArraySize.benchLoop 10485760 avgt 25 1.905 ± 0.078 ns/op
ArraySize.benchLoop 16777216 avgt 25 4.451 ± 0.287 ns/op
ArraySize.benchLoop 33554432 avgt 25 4.932 ± 0.030 ns/op
ArraySize.benchLoop 67108864 avgt 25 5.125 ± 0.041 ns/op
ArraySize.benchLoop 134217728 avgt 25 5.177 ± 0.020 ns/op
ArraySize.benchLoop 268435456 avgt 25 5.201 ± 0.033 ns/op
ArraySize.benchLoop 536870912 avgt 25 5.320 ± 0.274 ns/op
Как известно, доступ к одному элементу требует постоянного времени в нотации Big O O(1). Но на аппаратном уровне мы получаем различные уровни кэша, которые имеют разное время доступа к хранимым данным. Если мы выполняем итерацию в кэше L1-L3, то на эту операцию уходит менее 2 нс/оп. Но когда мы загружаем данные из оперативной памяти, это занимает больше времени. Если присмотреться, то можно заметить небольшой переход между кэшами L1, L2 и L3: время доступа увеличивается от L1 к L3 кэшу.
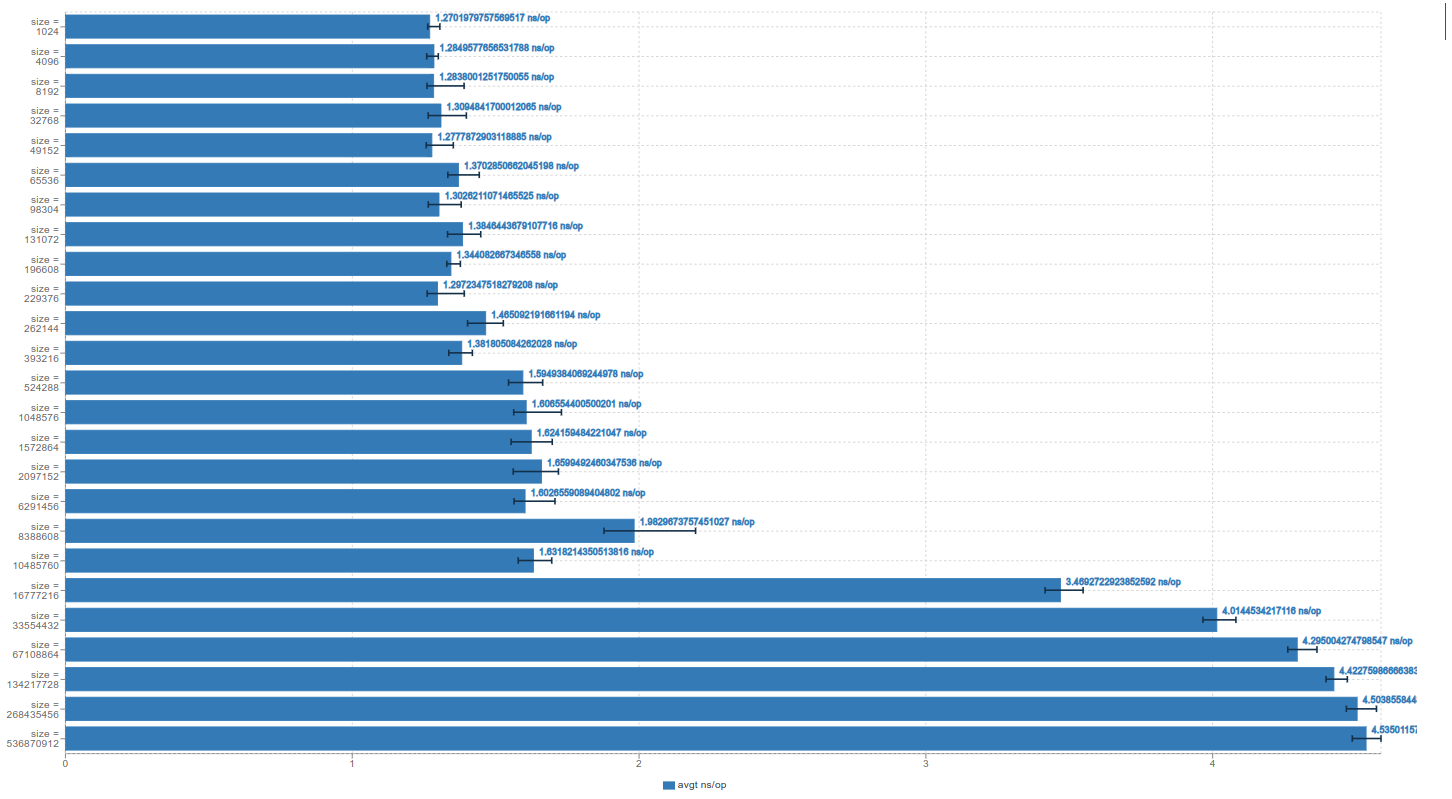
Размер имеет значение. Чем меньше объем данных, используемых для той или иной структуры данных, тем выше вероятность того, что они поместятся в кэш, что может привести к значительному повышению производительности.
Схемы доступа к данным. Произвольный или последовательный доступ к памяти
Does the order in which you access your data have an influence, too? Instead of simply running an index through the array, create a second array that stores the access order. Access the array sequentially as before for one time, and then access it randomly and measure the difference. Take a look on listing below. Влияет ли порядок доступа к данным? Вместо того чтобы просто пробегать последовательно по массиву, создаем второй массив, в котором будет храниться порядок доступа к данным. В первом случае обратимся к массиву последовательно, как и раньше, а затем обратитесь к нему в произвольном порядке и измерем разницу. Посмотрите на листинг ниже.
@State(Scope.Thread)
@BenchmarkMode(Mode.AverageTime)
@Warmup(iterations = 5, time = 1)
@Measurement(iterations = 5, time = 1)
@OutputTimeUnit(TimeUnit.NANOSECONDS)
public class RandomAccess {
private static final int ARRAY_CONTENT = 777;
@Param({"1024", "2048", "4096", "8192", "16384", "32768", "65536", "131072", "262144", "524288", "1048576", "2097152", "4194304", "8388608", "16777216", "33554432", "67108864", "134217728", "268435456", "536870912"})
public int size;
public int[] array;
public int seqcounter;
public int randomcounter;
public int mask;
public int[] rndIndex;
public int[] seqIndex;
@Setup(Level.Iteration)
public void setUp() {
final int elements = size / 4;
final int indexes = elements / 16;
mask = indexes - 1;
array = new int[elements];
Arrays.fill(array, ARRAY_CONTENT);
rndIndex = new int[indexes];
seqIndex = new int[indexes];
seqcounter = 0;
randomcounter = 0;
final List<Integer> list = new ArrayList<>(indexes);
for (int i=0; i<indexes; i++) {
list.add(16 * i);
}
Collections.shuffle(list);
for (int i=0; i<indexes; i++) {
rndIndex[i] = list.get(i);
}
for (int i = 0; i < indexes; i++) {
seqIndex[i] = i*16;
}
}
@Benchmark
public void randomAccess(Blackhole bh) {
array[rndIndex[randomcounter]] *= 3;
randomcounter = (randomcounter + 1) & mask;
}
@Benchmark
public void seqAccess(Blackhole bh) {
array[seqIndex[seqcounter]] *= 3;
seqcounter = (seqcounter + 1) & mask;
}
}
Benchmark (size) Mode Cnt Score Error Units
RandomAccess.randomAccess 1024 avgt 25 1.511 ± 0.146 ns/op
RandomAccess.randomAccess 2048 avgt 25 1.472 ± 0.034 ns/op
RandomAccess.randomAccess 4096 avgt 25 1.448 ± 0.063 ns/op
RandomAccess.randomAccess 8192 avgt 25 1.429 ± 0.010 ns/op
RandomAccess.randomAccess 16384 avgt 25 1.477 ± 0.028 ns/op
RandomAccess.randomAccess 32768 avgt 25 1.588 ± 0.031 ns/op
RandomAccess.randomAccess 65536 avgt 25 1.671 ± 0.108 ns/op
RandomAccess.randomAccess 131072 avgt 25 1.736 ± 0.112 ns/op
RandomAccess.randomAccess 262144 avgt 25 2.256 ± 0.047 ns/op
RandomAccess.randomAccess 524288 avgt 25 2.559 ± 0.104 ns/op
RandomAccess.randomAccess 1048576 avgt 25 2.708 ± 0.084 ns/op
RandomAccess.randomAccess 2097152 avgt 25 2.746 ± 0.051 ns/op
RandomAccess.randomAccess 4194304 avgt 25 2.762 ± 0.089 ns/op
RandomAccess.randomAccess 8388608 avgt 25 5.918 ± 1.037 ns/op
RandomAccess.randomAccess 16777216 avgt 25 13.802 ± 0.815 ns/op
RandomAccess.randomAccess 33554432 avgt 25 14.856 ± 0.449 ns/op
RandomAccess.randomAccess 67108864 avgt 25 15.767 ± 0.647 ns/op
RandomAccess.randomAccess 134217728 avgt 25 16.016 ± 0.488 ns/op
RandomAccess.randomAccess 268435456 avgt 25 16.138 ± 0.322 ns/op
RandomAccess.randomAccess 536870912 avgt 25 16.286 ± 0.264 ns/op
RandomAccess.seqAccess 1024 avgt 25 1.480 ± 0.026 ns/op
RandomAccess.seqAccess 2048 avgt 25 1.462 ± 0.024 ns/op
RandomAccess.seqAccess 4096 avgt 25 1.449 ± 0.018 ns/op
RandomAccess.seqAccess 8192 avgt 25 1.452 ± 0.041 ns/op
RandomAccess.seqAccess 16384 avgt 25 1.518 ± 0.113 ns/op
RandomAccess.seqAccess 32768 avgt 25 1.521 ± 0.011 ns/op
RandomAccess.seqAccess 65536 avgt 25 1.642 ± 0.054 ns/op
RandomAccess.seqAccess 131072 avgt 25 1.664 ± 0.044 ns/op
RandomAccess.seqAccess 262144 avgt 25 1.785 ± 0.030 ns/op
RandomAccess.seqAccess 524288 avgt 25 1.928 ± 0.041 ns/op
RandomAccess.seqAccess 1048576 avgt 25 1.989 ± 0.074 ns/op
RandomAccess.seqAccess 2097152 avgt 25 2.029 ± 0.100 ns/op
RandomAccess.seqAccess 4194304 avgt 25 2.077 ± 0.097 ns/op
RandomAccess.seqAccess 8388608 avgt 25 2.827 ± 0.328 ns/op
RandomAccess.seqAccess 16777216 avgt 25 5.133 ± 0.480 ns/op
RandomAccess.seqAccess 33554432 avgt 25 5.680 ± 0.352 ns/op
RandomAccess.seqAccess 67108864 avgt 25 5.599 ± 0.374 ns/op
RandomAccess.seqAccess 134217728 avgt 25 5.353 ± 0.441 ns/op
RandomAccess.seqAccess 268435456 avgt 25 5.236 ± 0.330 ns/op
RandomAccess.seqAccess 536870912 avgt 25 5.053 ± 0.145 ns/op
В результате обе кривые показывают практически одинаковое время доступа на с кэшами L1, L2 и L3.
Производительность схемы последовательного доступа заметно выше чем в произвольном, оссобенно заметно при загрузке данных из памяти.
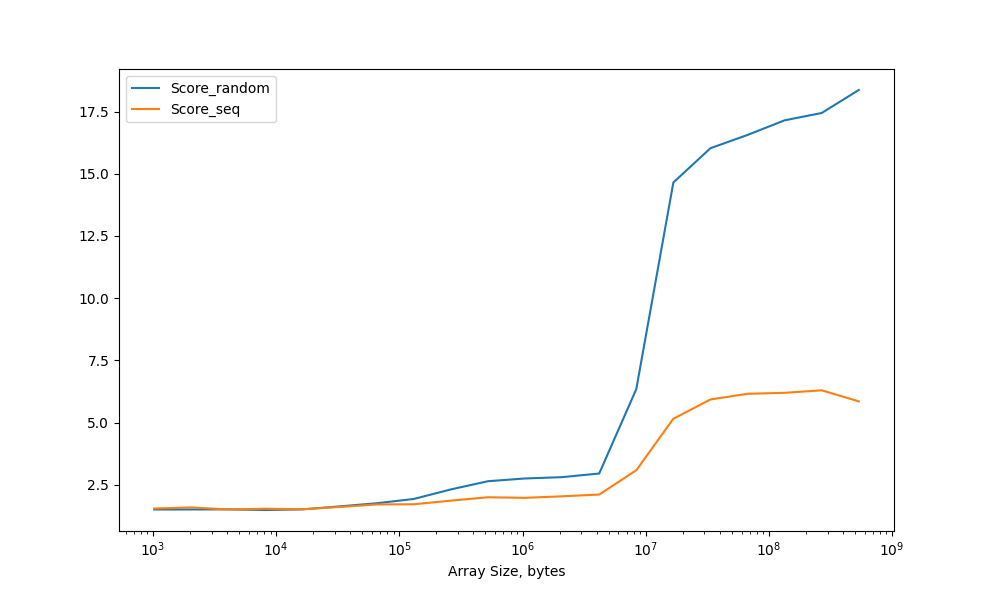
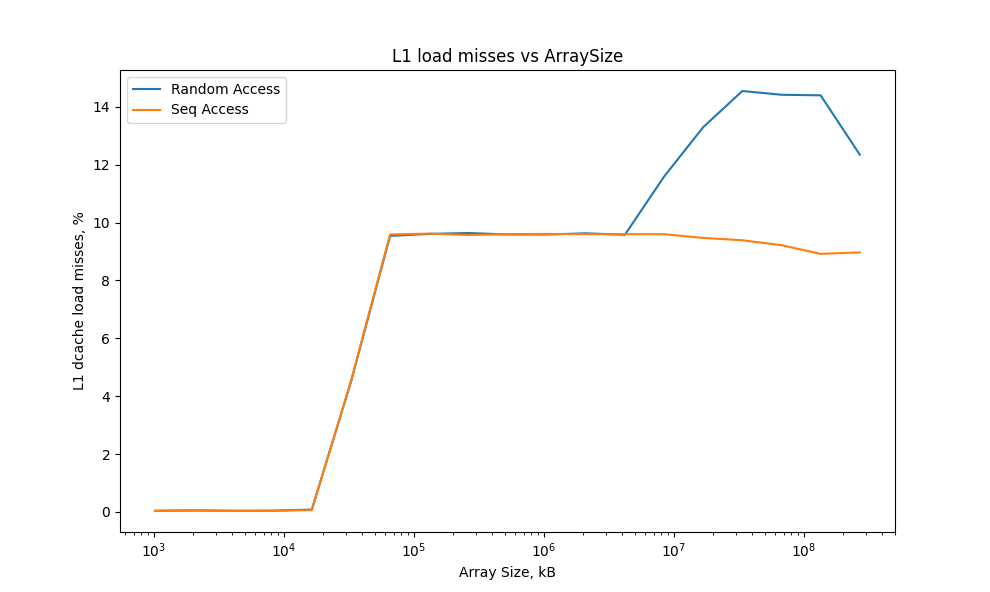
Соотношение между успешными загрузками и промахами кэш-памяти очень сильно отличается при разном доступе к данным. При последовательном обращении к массиву только около 6% всех загрузок памяти приводят к cache miss. При случайном обращении к данным количество промахов кэш-памяти возрастает. Большое количество cache miss вполне ожидаемо, поскольку массив не помещается в кэш, и приходится загружать все из оперативной памяти. Но почему при последовательном обращении к массиву промахов в кэше практически нет? Потому что есть префетчер, который загружает данные следующей строки кэша при взаимодействии с текущей строкой. Именно поэтому при последовательном доступе к массиву небольшого размера мы можем наблюдать низкий уровень cache miss.
Снижение производительности при False Sharing
@State(Scope.Group)
@BenchmarkMode(Mode.Throughput)
@OutputTimeUnit(TimeUnit.MICROSECONDS)
@Warmup(iterations = 5, time = 1, timeUnit = TimeUnit.SECONDS)
@Measurement(iterations = 5, time = 1, timeUnit = TimeUnit.SECONDS)
@Fork(2)
@Threads(2)
public class FalseSharing {
public final int[] array = new int[17];
@Benchmark
@Group("near")
@GroupThreads(1)
public void modifyNearA() {
array[0]++;
}
@Benchmark
@Group("near")
@GroupThreads(1)
public void modifyNearB() {
array[1]++;
}
@Benchmark
@Group("far")
@GroupThreads(1)
public void modifyFarA() {
array[0]++;
}
@Benchmark
@Group("far")
@GroupThreads(1)
public void modifyFarB() {
array[16]++;
}
}
Benchmark Mode Cnt Score Error Units
FalseSharing.baseline thrpt 25 1648.375 ± 531.950 ops/us
FalseSharing.baseline:reader thrpt 25 801.301 ± 522.013 ops/us
FalseSharing.baseline:writer thrpt 25 847.073 ± 14.666 ops/us
FalseSharing.far thrpt 25 536.287 ± 66.998 ops/us
FalseSharing.far:modifyFarA thrpt 25 372.084 ± 45.881 ops/us
FalseSharing.far:modifyFarB thrpt 25 164.203 ± 52.845 ops/us
FalseSharing.near thrpt 25 407.426 ± 48.644 ops/us
FalseSharing.near:modifyNearA thrpt 25 230.663 ± 43.739 ops/us
FalseSharing.near:modifyNearB thrpt 25 176.763 ± 41.006 ops/us